埋め込み境界法(IBM)とは
埋め込み境界法(IBM)とは流体の支配方程式に対し仮想外力項を加えることで、物体境界を再現する方法です。外力項を加える方法はさまざまなため、一言でIBM といっても中身は大きく異る場合があります。
カットセル技術が流体シミュレーションに導入さたのは、NASA のM. J. Aftosmis 率いるCart3D プロジェクトが最初です。当時(1995年頃)のCart3D は非粘性圧縮流れを取り扱う3次元ソフトでしたが、現在は粘性流れの数値解析まで対応しています。Cart3Dの計算格子一例を図3 に示します。( http://people . nas .nasa . gov/ ~aftosmis/cart
3d/より引用)

図3 Cart3Dによる格子作成一例
Cart3Dの成功がきっかけとなり、2000年前後にアメリカを中心としてカットセル法、IBMに代表される直交格子に関する研究ブームがおき、多くの研究成果が発表されました。日本でも直交格子の研究が活発化され、計算力学やCFD学会ではしばしば直交格子法単独のセッションまで設けられるようになりました。
直交格子法は通常八分木法(Octree 法)と組み合わせて使われます。
Octree のイメージを図4 に示します。イメージとおり、一個の格子を八個に分割し、目標細かさまで分割していきます。図3 で取り上
げたCart3D の事例は
Octree 法が導入された直交格子です。Octree 法はの格子数を著しく下げられることで知られています。
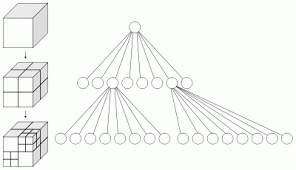
図4 八分木(Octree)のイメージ
直交格子をメインで使用しているPHOENICSはカットセル法とIBM両方搭載しています。PHOENICSではそれぞれPARSOL法とSPARSOL法とよんでいます。
カットセル法やIBMを導入した直交格子を採用している商用ソフトとしてPHOENICS以外にFLUENT(Ansys社)、STREAM(Cradle社)、FlowSimulation(SolidWorks社)、FloEFD(Mentor Graphics社)などがあります。カットセル法やIBMを導入することにより直交格子の適用分野が広がる気がしますが、計算精度はどうなるのでしょうか?今回は非圧縮層流の2次元並行平板間ポアズイユ流れよりカットセルの計算精度を検証することにします。十分発達した平行平板
間の幅(y)方向の速度の厳密解は式(1)になります。ただし、uは主流方向速度、xは流れ方向座標、yは流れに垂直方向座標、h平板間距離、μは流体の粘性係数、pは流体の圧力です。式(1)から、十分発達した平行平板間の中心線上速度は平均速度の1.5倍になります。

 
図5 計算格子 図6 速度ベクトル
平板の長さを1m、入り口平均流速を0.01m/sに設定し、計算を行いました。
図5、図6はそれぞれカットセル法を用いた計算格子とその計算結果である速度ベクトル図です。図7 二次元断面速度分布を示します。実線は式(1)の厳密解、赤丸は計算結果です。計算結果と厳密解との良好な一致が確認でき、流速の最大誤差が1%以内に収まっていることが分かります。
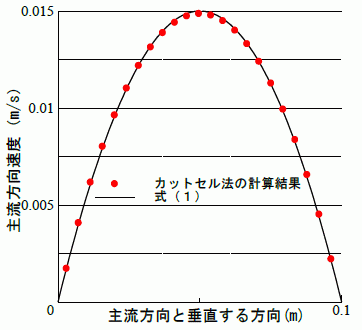
図7 断面速度分布
|