Dr. R. P. Hornby (Retired Research Engineer, ex DSTL, DERA & NNC)
はじめに
流体の波動をシミュレートする場合、領域境界で反射した波、特にこれらの波が必要なシミュレーションの一部を形成していない場合に問題が発生する可能性があります。このような反射波が流れのシミュレーションに与える影響を最小限に抑えるために、さまざまな手法が採用されてきました [1]。原理的には、反射が十分に弱くなる距離まで領域を拡張できますが、計算コストが高くなります。最も一般的な方法では、境界に沿ってスポンジ層を配置し、運動量方程式に抵抗源項を配置して、入射波エネルギーを吸収するように設計されています。この記事では、内部波流のPHOENICSシミュレーションにおけるこのような方法の使用について説明しますが、これらの方法は他の波動にも同様に有効です。
解析方法
簡略化のため、一様成層環境下で振動する物体について、2次元の時間依存解析を行う。PHOENICSで、直交座標系とKOREN差分法を用い時間依存の層流方程式(質量、運動量、エネルギー)を解きます。x、y、z座標は、それぞれ横方向と縦方向にとり、z座標は振動方向とする。局所的な浮力周波数は次式で与えられます。

ここでgは重力加速度、ρは密度、Nは定数です。振動体の場合、N[2]未満の周波数の波は垂直方向に現れます。
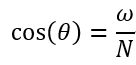
領域境界における波の減衰を調べるため、上下の境界(波の反射が起こる場所)に沿ってスポンジ層を配置します。このスポンジ層では、線形または二次の抵抗力項、あるいはその両方を適用できます。もしくは、スポンジ層内の流体粘性を高めることでも同様の結果が得ることが期待できます。
単位体積あたりの線形抵抗力項は、次の式で表わされます。
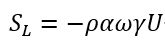
ここでUは速度の垂直または水平成分です。
単位体積あたりの二次の抵抗力項は次のようになります。

ここで、U は速度の垂直成分または水平成分、α と β は正の無次元定数、k は波数、γ はスポンジ層内で 0 から 1 まで徐々に増加するブレンディング関数です。
[1]に示されている適切なブレンディング関数は
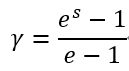
ここで
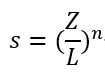
Zは厚さLのスポンジ層までの距離であり、n は混合の度合いを制御する定数 (通常は 1、2、または 4) であり、n の値が大きいほど、距離に応じて緩やかな減衰が生成されます。
粘性減衰の場合、スポンジ層の運動量方程式における層流動粘性は次のように表わされます。
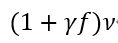
ここで、fは無次元粘性増加係数であり、νはスポンジ層外の層流動粘性係数である。fの大まかな推定値は以下の通りです。
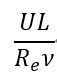
ここで、U と L は局所的な速度と長さのスケールであり、Re は粘性効果が優勢であることを示す指定された局所的なレイノルズ数 <1 です。
すべてのケースにおいて、α、βとfの値はある程度の試行錯誤を必要としますが、前者の2つのパラメータはO(1)にすると反射波が発生すると予想されます。
計算結果
シミュレーションは実際には無限領域にわたって行われる必要がありますが、実際には有限の計算時間でモデル化できるのは有限領域のみです。図1は、鉛直Z方向に均一に成層した流体で満たされたモデル化領域を示しています。上記の解析を用いた例示的な結果を図1に示します。
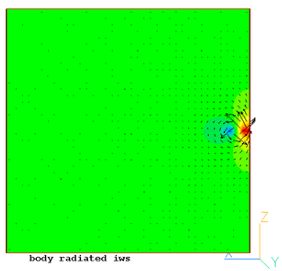
図1. 内部波減衰シミュレーションの2次元領域 (振動体は領域の右側中央に配置)
垂直方向に振動する正弦波の周波数ソースnを使用して、領域の境界をはるかに下ります。
ωの値は、振動体のサイズに関連する波数 k を持つ、垂直に対して 45 度の方向を向いた内部波のビームを生成するために取られます。図からわかるように、内部波のエネルギーは垂直に対して45度のビーム状に伝わり、上面と下面の境界で反射し、後方に関しては下流の境界で反射して、発生源の位置に戻ります。
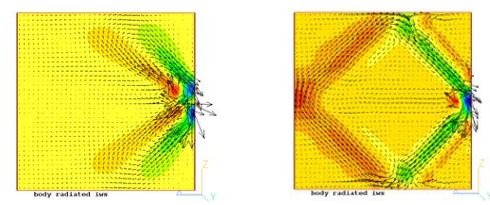
図 2 (a) 発生源から発せられ、上部境界と下部境界に向かって移動する内部波ビームの速度ベクトルと速度コンタ図
図 2 (b) 内部波ビームが上部境界、下部境界、および後方境界に到達し、反射した後の時刻の分布
これらの波の反射が望ましくない場合は、抑制する必要があります。これは、通常数波長の幅を持つスポンジ層を上下の境界に導入することで実現できます。スポンジ層内では、抵抗項が両方の運動量方程式のソース項として組み込まれます。あるいは、別の選択肢として、流体の粘性を大幅に増加させることもできます。図2bに対応する時刻に関して、3つの例示的なシミュレーションを実行したシミュレーション結果を以下に示します。
最初のシミュレーションでは、α、n = 1として線形ソース項が使用されています。結果は図3に示します。ご覧のとおり、反射波エネルギーが著しく減少しています。
2 番目のシミュレーションでは、図 4 は、β=7 にしたときの二次の減衰を使用した結果を示しています。ここでも、反射波エネルギーが大幅に減少しています。
3番目のシミュレーションではスポンジ層の粘性減衰を使用し、シミュレーション2と3で得られた結果と同様の結果が得られました(図5を参照)

図3.線形の減衰:シミュレーションで図2bと同じ時刻の内部波ビームの速度ベクトルと速度コンタ等
反射波エネルギーの顕著な減少を示している( α=1、n=1)

図4.二次の減衰:シミュレーションで図2bと同じ時刻の内部波ビームの速度ベクトルと速度コンタ等
反射波エネルギーの顕著な減少を示している( β=7、n=1)

図5.粘性による減衰:シミュレーションで図2bと同じ時刻の内部波ビームの速度ベクトルと速度コンタ等
反射波エネルギーの顕著な減少を示している
結論
運動量方程式に線形または二次の抵抗項を組み込んだスポンジ層を導入するか、流体の粘性を高めることで、境界からの内部波反射を大幅に低減できることが示されました。反射波の減衰の程度は、上記に示した無次元パラメータによって制御されますが、特定のシミュレーションに最適なパラメータを決定するには、ある程度の実験が必要です。同様の処理が、他の種類の流体波の境界反射を低減するのにも有効であることが期待されます。
参考文献
1.Peri?, R., & Abdel-Maksoud, M. (2016). Reliable damping of free-surface waves in numerical simulations. Ship Technology Research, 63(1),
2.Lighthill, M.J. (1978). Waves in fluids. Cambridge University Press.
|