| 目的: |
- PHOENICSで、同心環状空間での非ニュートン流体の粘性流れを計算した。
- 主な目的は、解析値や実験値とHerschel-Bulkley(HB)の流動モデルを用いた
PHOENICSの結果を比較することでPHOENICSの有効性を示すことである。
|
|
| 概要: |
- この問題はドリルで穴を空ける時のドリルラインと岩石の間の環状空間内の実際
の流れと関連しています。さらに正常な穿孔中にでもドリルラインは穴の中心には
ないことが知られています。
- 従って数値解析による予測は掘削技師にとって、特別な孔形状の場合に使用する
流体の流動性や流量を決定するための助けとなります。その結果、掘削、輸送は
効率よく行なえ、一方、環状の圧力が割れ目の下に残る 。
|
|
| 要点: |
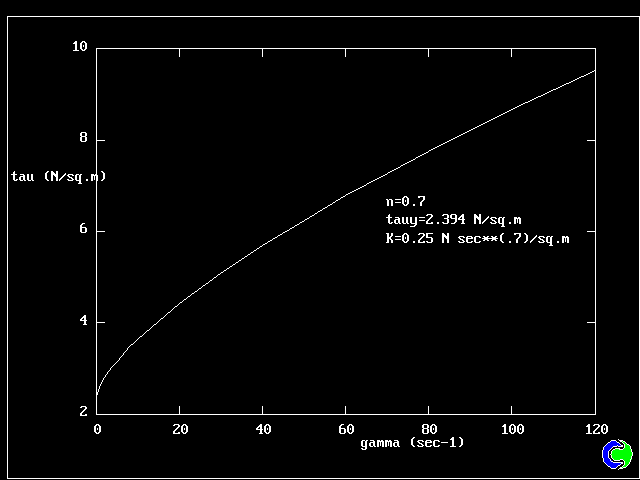
- HBモデルは、せん断応力τを、調和係数Kと降伏応力τy、べき乗指数nによって
歪み率γとを関連付ける。即ち、 τ= τy + K*(γ**n)
- HBモデルはτyが0のときのべき乗モデルを単純化します。例えば、値が n<1 なら
ば、流動は擬似塑性(せん断流動化)であり、n>1ならば、ダイラタント(せん断粘稠
化)である。
- 降伏応力を越えたときに流動が始まります。
- n=1の時、HBモデルはBingham plasitcモデルになります。
- τy=0、n=1の時、ニュートン流体になる。
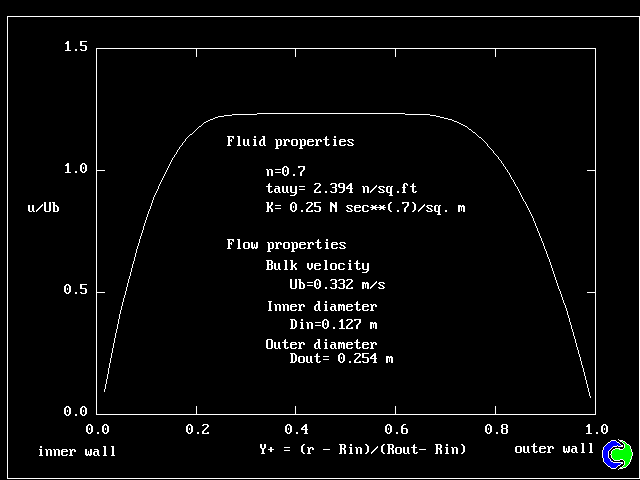
- 速度プロファイル、摩擦抵抗、圧力損失を計算するために、べき乗流体とHB流体
両方の完全に発達した層流流れとして単一平面ソルバーによって計算されます。
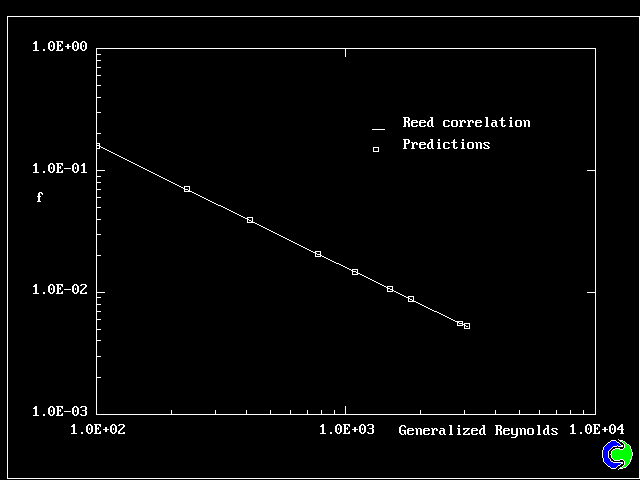
- そのパラメータは、摩擦係数 f と、孔の有効径に基づく一般的レイノルズ数GRE
である。 (参照: Reed & Pilehvari [1993]).
- 有効径は、孔の形状と流体の流動性の両方の関数として定義されます。Reed &
Pilhvari [1993]
- 摩擦係数 f の実験値は、f =16/GRE で与えられ、その結果はPHOENICSでも再現
できた。
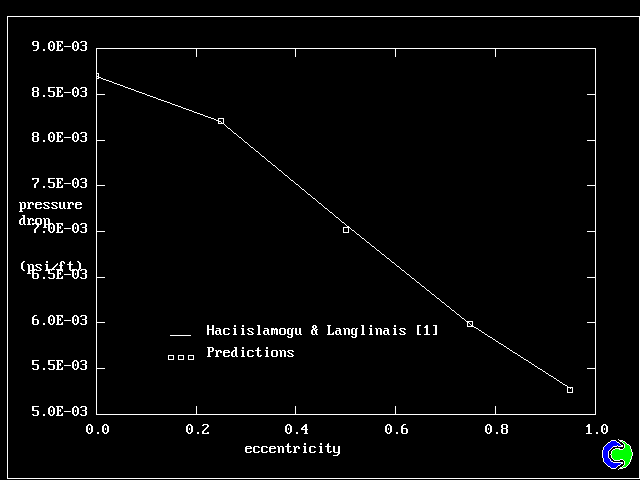
- PHOENICSの計算もまた、Quigleyら[SPE26343]のべき乗則値を求めるための
圧力降下−流量曲線のグラフを作成した。
|
|
| 結果: |
| 1. HERSCHEL-BULKLEY FLUID: 摩擦抵抗 |
|
|
|
| 2. HERSCHEL-BULKLEY FLUID: 流量曲線 |
|
|
|
| 3. HERSCHEL-BULKLEY FLUID: 速度分布 |
|
|
|
| 4. POWER-LAW FLUID: 圧力降下 vs 流量 |
|
|
|